Generating Extremely Long Sequences in JAX

Sasha Rush (@srush_nlp) with Sidd Karamcheti

https://github.com/srush/annotated-s4

Based on research by Albert Gu, Karan Goel, and Christopher Ré.

Intro

Intro

Talk Goals

Caveat: Not a research talk, there will be bugs 🧑‍🔬

    1. Learn about a new ML architecture.
    2. Understand how JAX supports it.

JAX: Pros and Cons

Cons

    • Debugging is still hard
    • No NN standard
    • Hard to reason about (for me)

Pros

    • Seperate math from NN (facilitates testing)
    • JIT is really impressive
    • Lifted transformations are magic

Problem Context

Sequence Modeling

Birds-Eye: Learning over a list of elements (discrete or sampled signal)

  • Classification

    Is the dog a good boy?

    • Yes

  • Generation

    The dog is a good _____

The Transformer

Transformer Dominance

isattentionallyouneed.com

The Transformer Weakness

  • Scales O(L2)O(L^2) with length LL.

Recurrent Neural Networks (RNN)

  • Scales O(L)O(L) with length LL.

Long Range Arena

  • A benchmark of extremely long sequence tasks (up to 16k tokens)

Linearized Images

Path-X

  • Classification problem on linearized (one pixel at a time) image sequence.

Method

Efficiently Modeling Long Sequences with Structured State Spaces

Albert Gu, Karan Goel, and Christopher Ré.

Punchline

Challenges

  • The model is quite mathematically complicated (want to test)
  • Core operations required external libraries in Torch
  • Follow-up work uses similar structure

Goal

  • A concise pedagogical JAX / Flax implementation.

The Annotated S4

Image Generation

Speech Generation

Part 1: SSM

State Space Models (SSM)

  • A state space model maps a 1-D input signal u(t)u(t) to an NN-D latent state x(t)x(t)
    before projecting to a 1-D output signal y(t)y(t).

x′(t)=Ax(t)+Bu(t)y(t)=Cx(t) \begin{aligned} x'(t) &= \boldsymbol{A}x(t) + \boldsymbol{B}u(t) \\ y(t) &= \boldsymbol{C}x(t)\\ \end{aligned}

  • A\boldsymbol{A}, B\boldsymbol{B}, C\boldsymbol{C} are parameters; uu input, yy output, xx state
def random_SSM(rng, N):
    a_r, b_r, c_r = jax.random.split(rng, 3)
    A = jax.random.uniform(a_r, (N, N))
    B = jax.random.uniform(b_r, (N, 1))
    C = jax.random.uniform(c_r, (1, N))
    return A, B, C

Discretization

  • To discretize input sequence (u0,u1,…,uL−1)(u_0, u_1, \dots, u_{L-1}) need a step size Δ\Delta representing uk=u(kΔ)u_k = u(k \Delta).

  • One choice for discretization is a bilinear transform.

A‾=(I−Δ/2⋅A)−1(I+Δ/2⋅A)B‾=(I−Δ/2⋅A)−1ΔBC‾=C\begin{aligned} \boldsymbol{\overline{A}} &= (\boldsymbol{I} - \Delta/2 \cdot \boldsymbol{A})^{-1}(\boldsymbol{I} + \Delta/2 \cdot \boldsymbol{A}) \\ \boldsymbol{\overline{B}} &= (\boldsymbol{I} - \Delta/2 \cdot \boldsymbol{A})^{-1} \Delta \boldsymbol{B} \\ \boldsymbol{\overline{C}} &= \boldsymbol{C}\\ \end{aligned} 

def discretize(A, B, C, step):
    I = np.eye(A.shape[0])
    BL = inv(I - (step / 2.0) * A)
    Ab = BL @ (I + (step / 2.0) * A)
    Bb = (BL * step) @ B
    return Ab, Bb, C

Discretized SSM as RNN

  • Once discretized with step Δ\Delta, the SSM can be viewed as a linear RNN,

xk=A‾xk−1+B‾ukyk=C‾xk\begin{aligned} x_{k} &= \boldsymbol{\overline{A}} x_{k-1} + \boldsymbol{\overline{B}} u_k\\ y_k &= \boldsymbol{\overline{C}} x_k \\ \end{aligned} 

def scan_SSM(Ab, Bb, Cb, u, x0):
    def step(x_k_1, u_k):
        x_k = Ab @ x_k_1 + Bb @ u_k
        y_k = Cb @ x_k
        return x_k, y_k

    return jax.lax.scan(step, x0, u)

Tangent: A Mechanics Example

  • Example from mechanics, mass on a spring

    • forward position y(t)y(t)
    • force u(t)u(t) is applied to this mass
    • parameterized by mass (mm), spring constant (kk), friction constant (bb)

my′′(t)=u(t)−by′(t)−ky(t)\begin{aligned} my''(t) = u(t) - by'(t) - ky(t) \end{aligned}

Tangent: A Mechanics Example [Matrix form]

my′′(t)=u(t)−by′(t)−ky(t)\begin{aligned} my''(t) = u(t) - by'(t) - ky(t) \end{aligned}

A=[01−k/m−b/m]B=[01/m]C=[10]\begin{aligned} \boldsymbol{A} &= \begin{bmatrix} 0 & 1 \\ -k/m & -b/m \end{bmatrix} \\ \boldsymbol{B} & = \begin{bmatrix} 0 \\ 1/m \end{bmatrix} & \boldsymbol{C} = \begin{bmatrix} 1 & 0 \end{bmatrix} \\ \end{aligned} 

def example_mass(k, b, m):
    A = np.array([[0, 1], [-k / m, -b / m]])
    B = np.array([[0], [1.0 / m]])
    C = np.array([[1.0, 0]])
    return A, B, C

Tangent: A Mechanics Example (with force)

@partial(np.vectorize, signature="()->()")
def example_force(t):
    x = np.sin(10 * t)
    return x * (x > 0.5)

def example_ssm(L=100):
    ssm = example_mass(k=40, b=5, m=1)

    # L samples of u(t).
    step = 1.0 / L
    ks = np.arange(L)
    u = example_force(ks * step)
    y = scan_SSM(*ssm, u)

Training SSMs

  • Our Goal: Train a neural network with SSMs
  • SSM RNNs: Fast for generation, but slow for training

Key Properties

  • SSM CNNs: Slow for generation, but fast for training
  • Initilization

SSMs as wide CNNs

  1. "Unroll" the RNN representation

xk=A‾xk−1+B‾ukyk=C‾xk\begin{aligned} x_{k} &= \boldsymbol{\overline{A}} x_{k-1} + \boldsymbol{\overline{B}} u_k\\ y_k &= \boldsymbol{\overline{C}} x_k \\ \end{aligned}

x0=B‾u0x1=A‾B‾u0+B‾u1x2=A‾2B‾u0+A‾B‾u1+B‾u2…y0=C‾B‾u0y1=C‾A‾B‾u0+C‾B‾u1y2=C‾A‾2B‾u0+C‾A‾B‾u1+C‾B‾u2…\begin{aligned} x_0 &= \boldsymbol{\overline{B}} u_0 & x_1 &= \boldsymbol{\overline{A}} \boldsymbol{\overline{B}} u_0 + \boldsymbol{\overline{B}} u_1 & x_2 &= \boldsymbol{\overline{A}}^2 \boldsymbol{\overline{B}} u_0 + \boldsymbol{\overline{A}} \boldsymbol{\overline{B}} u_1 + \boldsymbol{\overline{B}} u_2 & \dots \\ y_0 &= \boldsymbol{\overline{C}} \boldsymbol{\overline{B}} u_0 & y_1 &= \boldsymbol{\overline{C}} \boldsymbol{\overline{A}} \boldsymbol{\overline{B}} u_0 + \boldsymbol{\overline{C}} \boldsymbol{\overline{B}} u_1 & y_2 &= \boldsymbol{\overline{C}} \boldsymbol{\overline{A}}^2 \boldsymbol{\overline{B}} u_0 + \boldsymbol{\overline{C}} \boldsymbol{\overline{A}} \boldsymbol{\overline{B}} u_1 + \boldsymbol{\overline{C}} \boldsymbol{\overline{B}} u_2 & \dots \end{aligned}

SSMs as wide CNNs

  1. Form a LL-length kernel

yk=C‾A‾kB‾u0+C‾A‾k−1B‾u1+⋯+C‾A‾B‾uk−1+C‾B‾uk\begin{aligned} y_k &= \boldsymbol{\overline{C}} \boldsymbol{\overline{A}}^k \boldsymbol{\overline{B}} u_0 + \boldsymbol{\overline{C}} \boldsymbol{\overline{A}}^{k-1} \boldsymbol{\overline{B}} u_1 + \dots + \boldsymbol{\overline{C}} \boldsymbol{\overline{A}} \boldsymbol{\overline{B}} u_{k-1} + \boldsymbol{\overline{C}}\boldsymbol{\overline{B}} u_k \\ \end{aligned}

K‾∈RL=(C‾B‾,C‾A‾B‾,…,C‾A‾L−1B‾)\begin{aligned} \boldsymbol{\overline{K}} \in \mathbb{R}^L = (\boldsymbol{\overline{C}}\boldsymbol{\overline{B}}, \boldsymbol{\overline{C}}\boldsymbol{\overline{A}}\boldsymbol{\overline{B}}, \dots, \boldsymbol{\overline{C}}\boldsymbol{\overline{A}}^{L-1}\boldsymbol{\overline{B}}) \end{aligned} 

def K_conv(Ab, Bb, Cb, L):
    return np.array(
        [(Cb @ matrix_power(Ab, l) @ Bb).reshape() for l in range(L)]
    )

SSMs as wide CNNs

  1. Apply as a (non-cicular) convolution

y=K‾∗uy = \boldsymbol{\overline{K}} \ast u 

def non_circular_convolution(u, K, nofft=False):
    if nofft:
        return convolve(u, K, mode="full")[: u.shape[0]]
    else:
        ud = np.fft.rfft(np.pad(u, (0, K.shape[0])))
        Kd = np.fft.rfft(np.pad(K, (0, u.shape[0])))
        return np.fft.irfft(ud * Kd)[: u.shape[0]]
  • O(Llog⁡L)O(L \log L) training through FFT

Initialization with HiPPO

  • Fast training, but random init does terribly. MNIST classification benchmark 50%50\%.
  • HiPPO initialization of A\mathbf{A} improves this number to 98%98\%
def make_HiPPO(N):
    def v(n, k):
        if n > k:
            return np.sqrt(2 * n + 1) * np.sqrt(2 * k + 1)
        elif n == k:
            return n + 1
        else:
            return 0
    mat = [[v(n, k) for k in range(1, N + 1)] for n in range(1, N + 1)]
    return -np.array(mat)

HiPPO Intuition Sketch

  • Recall xkx_k is an NN-dimensional hidden representation of an LL-step signal
  • HiPPO approximates state as NN Legendre coefficients representing uu.

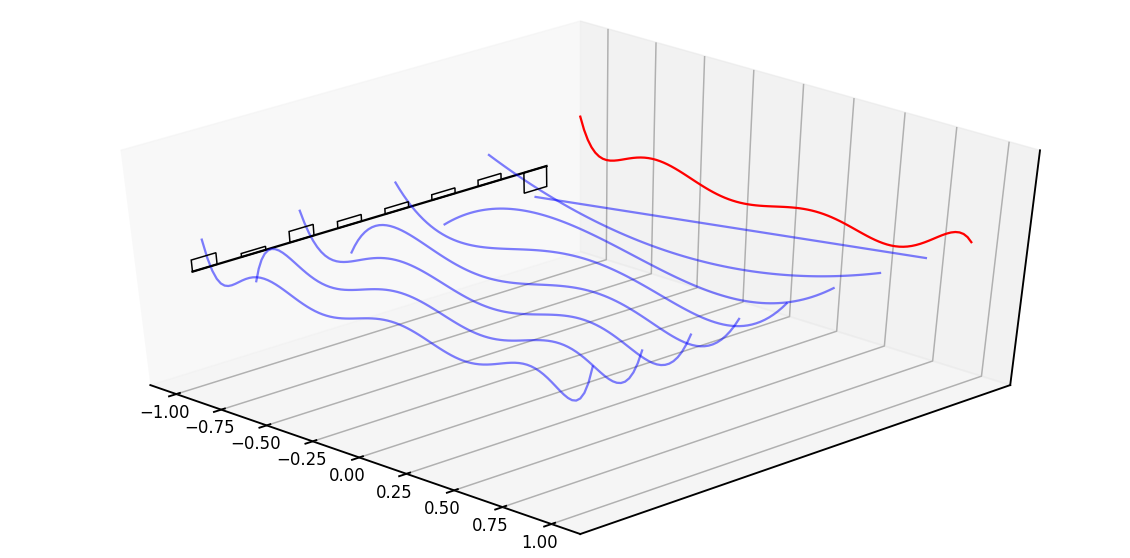
def example_legendre(N=8):
    u = (np.random.rand(N) - 0.5) * 2
    t = np.linspace(-1, 1, 100)
    x = numpy.polynomial.legendre.Legendre(u)(t)

Tangent: Neat JAX things.

  • Everything is a modular testable function
  • So far - no parameter, batches, NN nonsense
  • In fact, mostly scalar modeling.

SSM Network Layer

  • SSM layer with Flax (still scalar!)
class SSMLayer(nn.Module):
    A: np.DeviceArray  # HiPPO
    N, L: int

    def setup(self):
        self.B = self.param("B", lecun_normal(), (self.N, 1))
        self.C = self.param("C", lecun_normal(), (1, self.N))
        self.step = np.exp(self.param("log_step", log_step_initializer(), (1,)))

        # Conv created each time during training
        self.ssm = discretize(self.A, self.B, self.C, step=self.step)
        self.K = K_conv(*self.ssm, self.L)

    def __call__(self, u):
        return non_circular_convolution(u, self.K)

Lifting SSM Layer

  • Lift to HH copies
nn.vmap(
    layer, in_axes=1, out_axes=1,
    variable_axes={"params": 1}, # New Params
    split_rngs={"params": True},
)
  • Over BB batches
nn.vmap(
    layer, in_axes=0, out_axes=0,
    variable_axes={"params": None}, # Shared Params
    split_rngs={"params": False},
)
  • Put into a stack of layers (similar to Transformers)

SSM RNN Layer

  • Alternative SSM layer with Flax Caching
class SSMRNNLayer(nn.Module):
    A: np.DeviceArray  # HiPPO
    N, L: int

    def setup(self):
        self.B = self.param("B", lecun_normal(), (self.N, 1))
        self.C = self.param("C", lecun_normal(), (1, self.N))
        self.step = np.exp(self.param("log_step", log_step_initializer(), (1,)))
        self.ssm = discretize(self.A, self.B, self.C, step=self.step)
        self.x_k_1 = self.variable("cache", "cache_x_k", np.zeros, (self.N,))

    def __call__(self, u):
        x_k, y_s = scan_SSM(*self.ssm, u[:, np.newaxis], self.x_k_1.value)
        if self.is_mutable_collection("cache"):
           self.x_k_1.value = x_k
        return y_s.reshape(-1).real + self.D * u

Part 2: S4

Issue: Calculating KK

  • Unfortunately, this step is a problem.
def K_conv(Ab, Bb, Cb, L):
    return np.array(
        [(Cb @ matrix_power(Ab, l) @ Bb).reshape() for l in range(L)]
    )

  • Main contribution of S4 is to fix this function.

  • Today: quick sketch of how it works

Two S4 Tricks

See blog post for full details. Here are two neat JAX tricks.

  • Instead of computing K‾\boldsymbol{\overline{K}} directly, S4 evaluates its truncated generating function.

    • This becomes a functional vmap in JAX.

  • In order to evalute the generating function it computes a Cauchy kernel 1ωj−ζk\frac{1}{\omega_j - \zeta_k}.

    • This is intractable in Torch, but is jitted out in JAX.

Trick 1. SSM Generating Functions

The truncated SSM generating function at node zz with truncation LL is

K^L(z;A‾,B‾,C‾)∈C:=∑i=0L−1C‾A‾iB‾zi\hat{\mathcal{K}}_L(z; \boldsymbol{\overline{A}}, \boldsymbol{\overline{B}}, \boldsymbol{\overline{C}}) \in \mathbb{C} := \sum_{i=0}^{L-1} \boldsymbol{\overline{C}} \boldsymbol{\overline{A}}^i \boldsymbol{\overline{B}} z^i 

def K_gen_naive(Ab, Bb, Cb, L):
    K = K_conv(Ab, Bb, Cb, L)
    return lambda z: np.sum(K * (z ** np.arange(L)))

Trick 1. SSM Generating Functions

We can recover the kernel K{\cal K} through a z-transform at the roots of unity
Ω={exp⁡(2πkL:k∈[L]}\Omega = \{ \exp(2\pi \frac{k}{L} : k \in [L] \} and inverse fourier transformation.

def conv_from_gen(gen, L):
    Omega_L = np.exp((-2j * np.pi) * (np.arange(L) / L))
    atRoots = jax.vmap(gen)(Omega_L)
    return np.fft.ifft(atRoots, L).reshape(L).real

Trick 1. SSM Generating Functions

Simplifying the generating function allows us to avoid calling K_conv

K^L(z)=∑i=0L−1C‾A‾iB‾zi=C‾(I−A‾LzL)(I−A‾z)−1B‾\hat{\mathcal{K}}_L(z) = \sum_{i=0}^{L-1} \boldsymbol{\overline{C}} \boldsymbol{\overline{A}}^i \boldsymbol{\overline{B}} z^i = \boldsymbol{\overline{C}} (\boldsymbol{I} - \boldsymbol{\overline{A}}^L z^L) (\boldsymbol{I} - \boldsymbol{\overline{A}} z)^{-1} \boldsymbol{\overline{B}} 

def K_gen_inverse(Ab, Bb, Cb, L):
    I = np.eye(Ab.shape[0])
    Ab_L = matrix_power(Ab, L)
    Ct = Cb @ (I - Ab_L)
    return lambda z: (Ct.conj() @ inv(I - Ab * z) @ Bb).reshape()

Trick 2. Exploiting Structure

Under a diagonal assumption on A=Λ\mathbf{A}=\Lambda you can further reduce the generating function to the following kernel form,

K^Λ(z)=c(z)∑iC~iBi(g(z)−Λi) \begin{aligned} \boldsymbol{\hat{K}}_{\boldsymbol{\Lambda}}(z) & = c(z) \sum_i \frac{\tilde{C}_i B_i} {(g(z) - \Lambda_{i})} \\ \end{aligned}

where cc is a constant, and gg is a function of zz.

  • However the transform of this function is memory and compute-intensive.

    • L=16,000L=16,000 different zz, NN different ii
    • Instantiating full tensor is intractable
    • Libraries like KeOps avoid this issue

Trick 2. Exploiting Structure

In JAX we can rely on the JIT to take care of this for us.

  • JIT handles the fusion of the sum term
@partial(np.vectorize, signature="(c),(),(c)->()")
def cauchy_dot(v, omega, lambd):
    return (v / (omega - lambd)).sum()
  • JAX remat handles cases of very long sequences.
jax.remat(cauchy_dot)

Part 3: S4 in Practice

Training S4

  • So far: tested code for training S4 as a CNN and running it as an RNN.
  • MNIST classification and CIFAR classification (by pixel) are strong.

Goal

  • Generate extremely long sequences.

  • Expreriments on MNIST, QuickDraw, SpeechCommands

S4 Model

Training to Generate by Pixeal

Code to sample from the RNN

def sample(model, params, prime, cache, x, start, end, rng):
    def loop(i, cur):
        x, rng, cache = cur
        r, rng = jax.random.split(rng)
        out, vars = model.apply(
            {"params": params, "cache": cache},
            x[:, np.arange(1, 2) * i],
            mutable=["cache"],
        )

        def update(x, out):
            p = jax.random.categorical(r, out[0])
            return x.at[i + 1, 0].set(p)

        x = jax.vmap(update)(x, out)
        return x, rng, vars["cache"].unfreeze()

    return jax.lax.fori_loop(start, end, loop, (x, rng, cache))[0]

Generating by Pixel

Prefix Generation

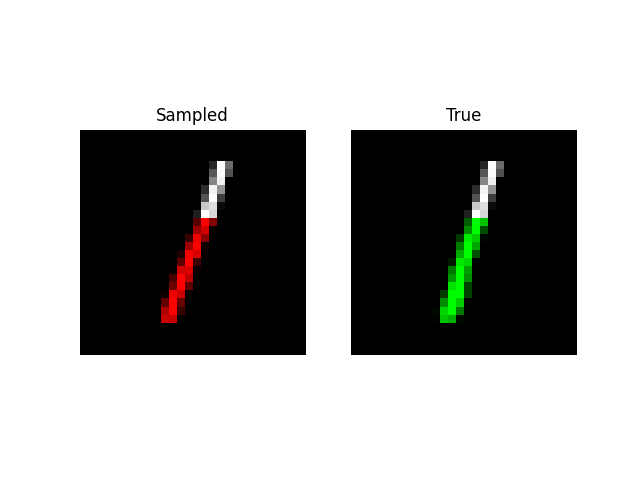
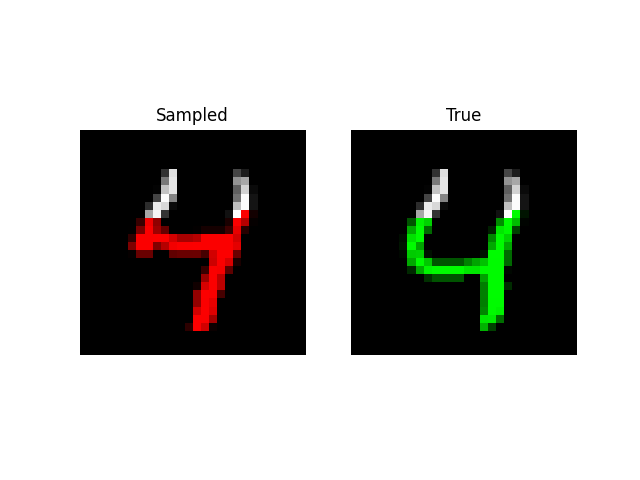
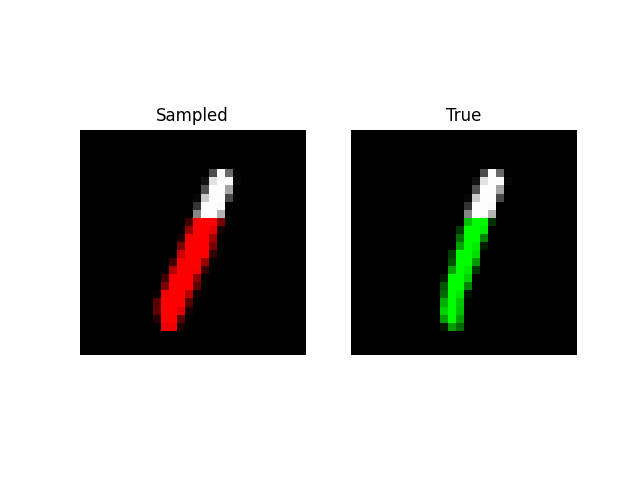
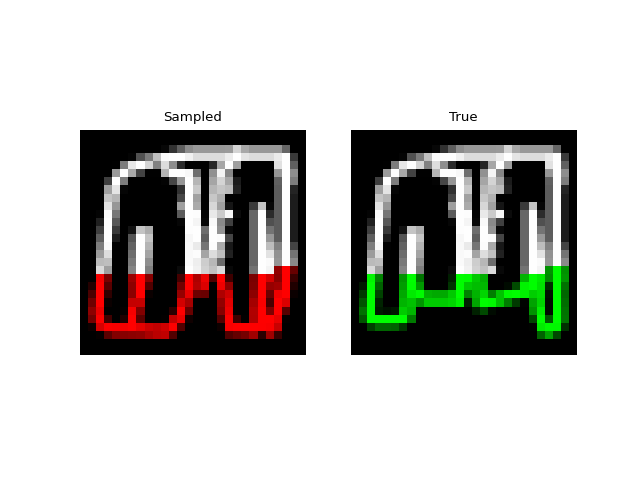
Experiments: QuickDraw

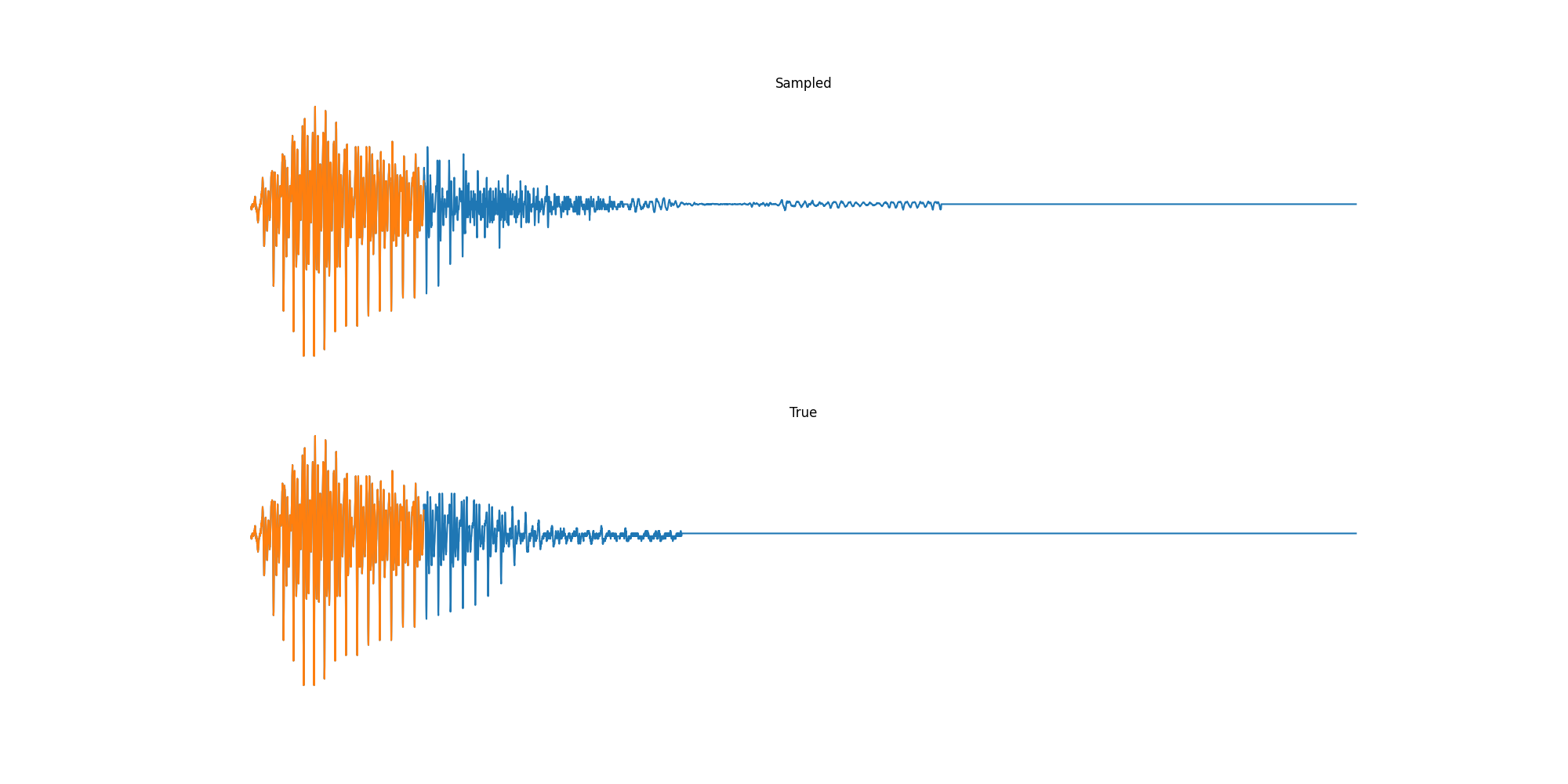
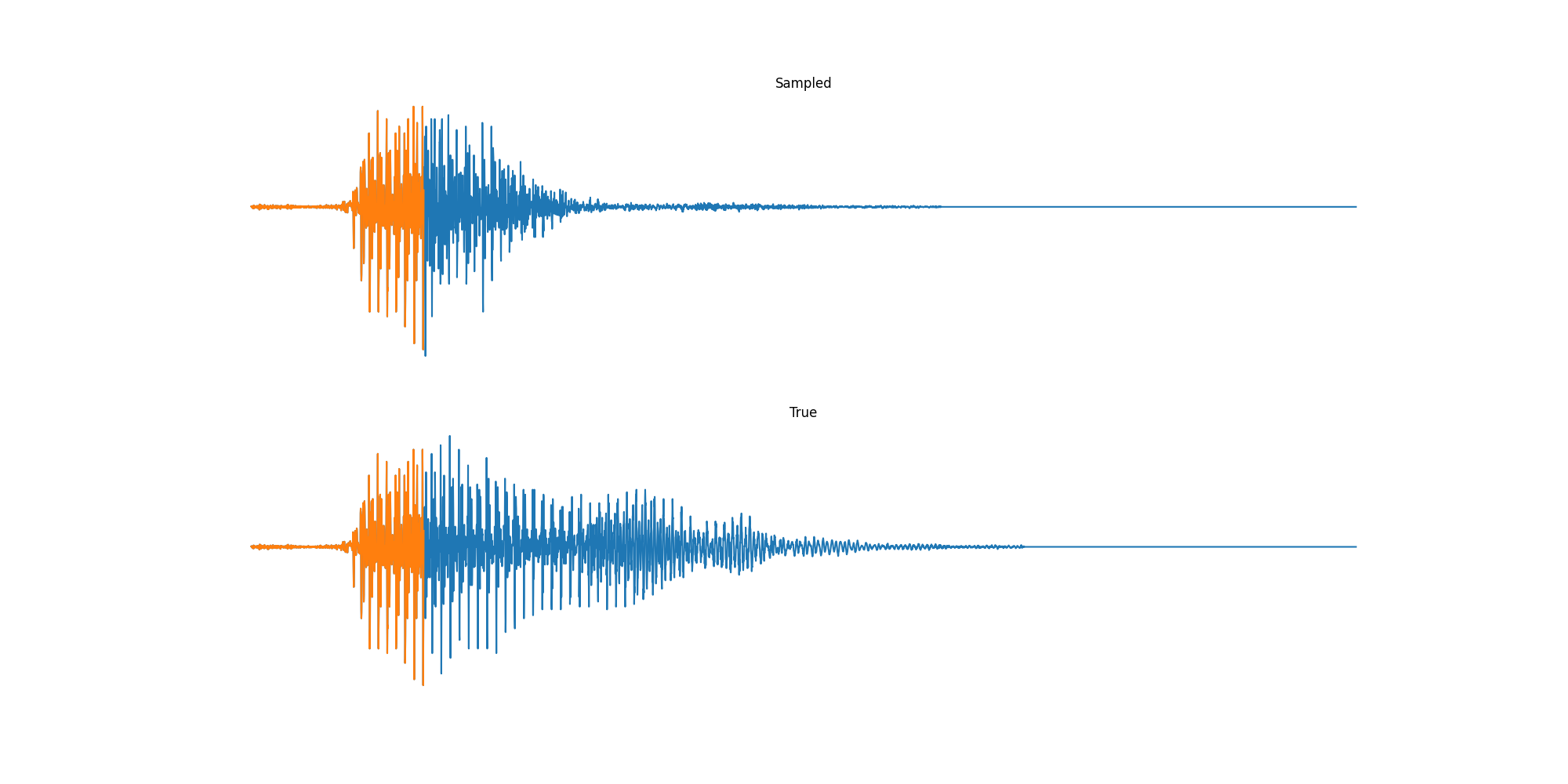
Experiments: Sound

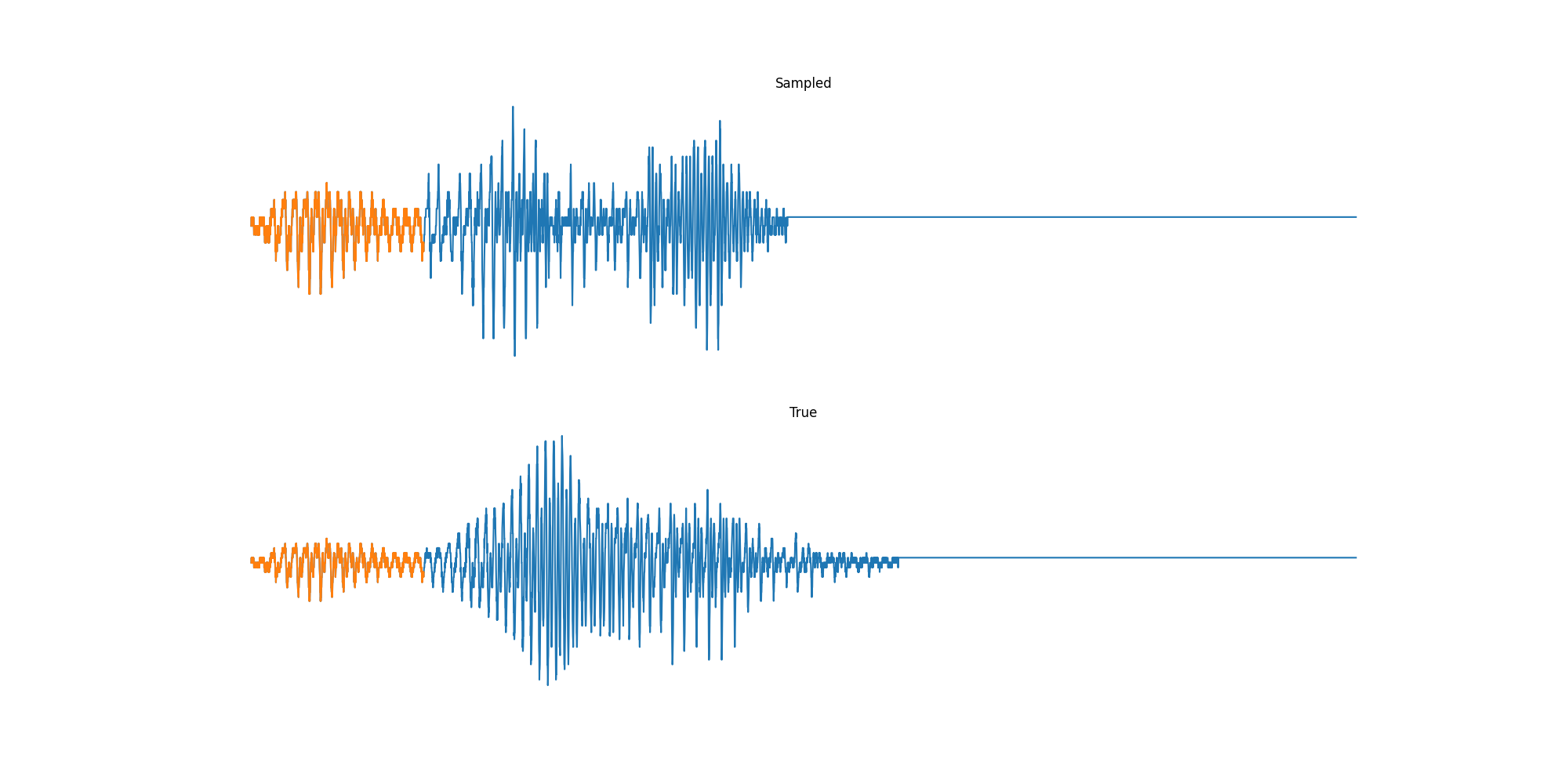
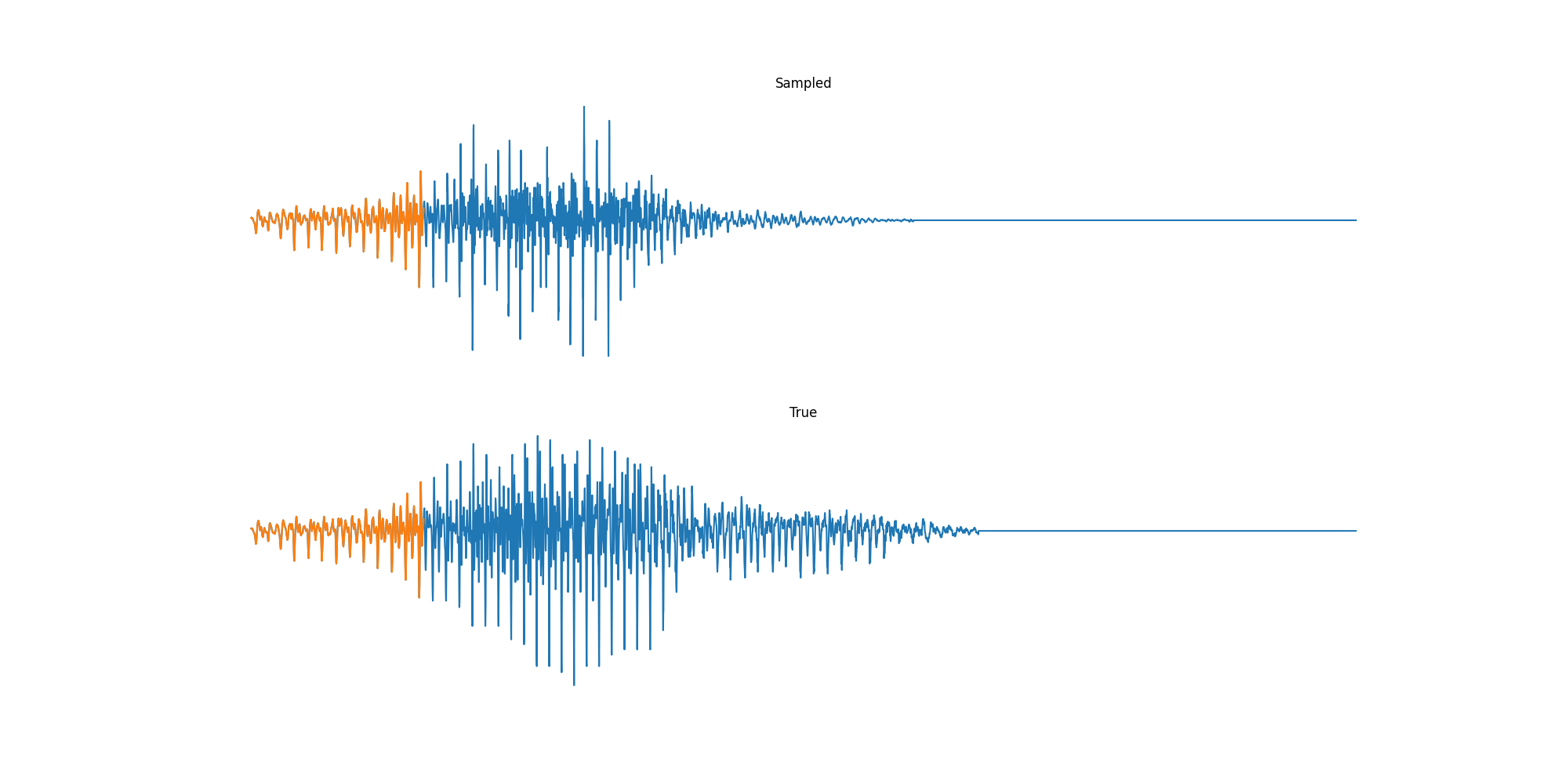
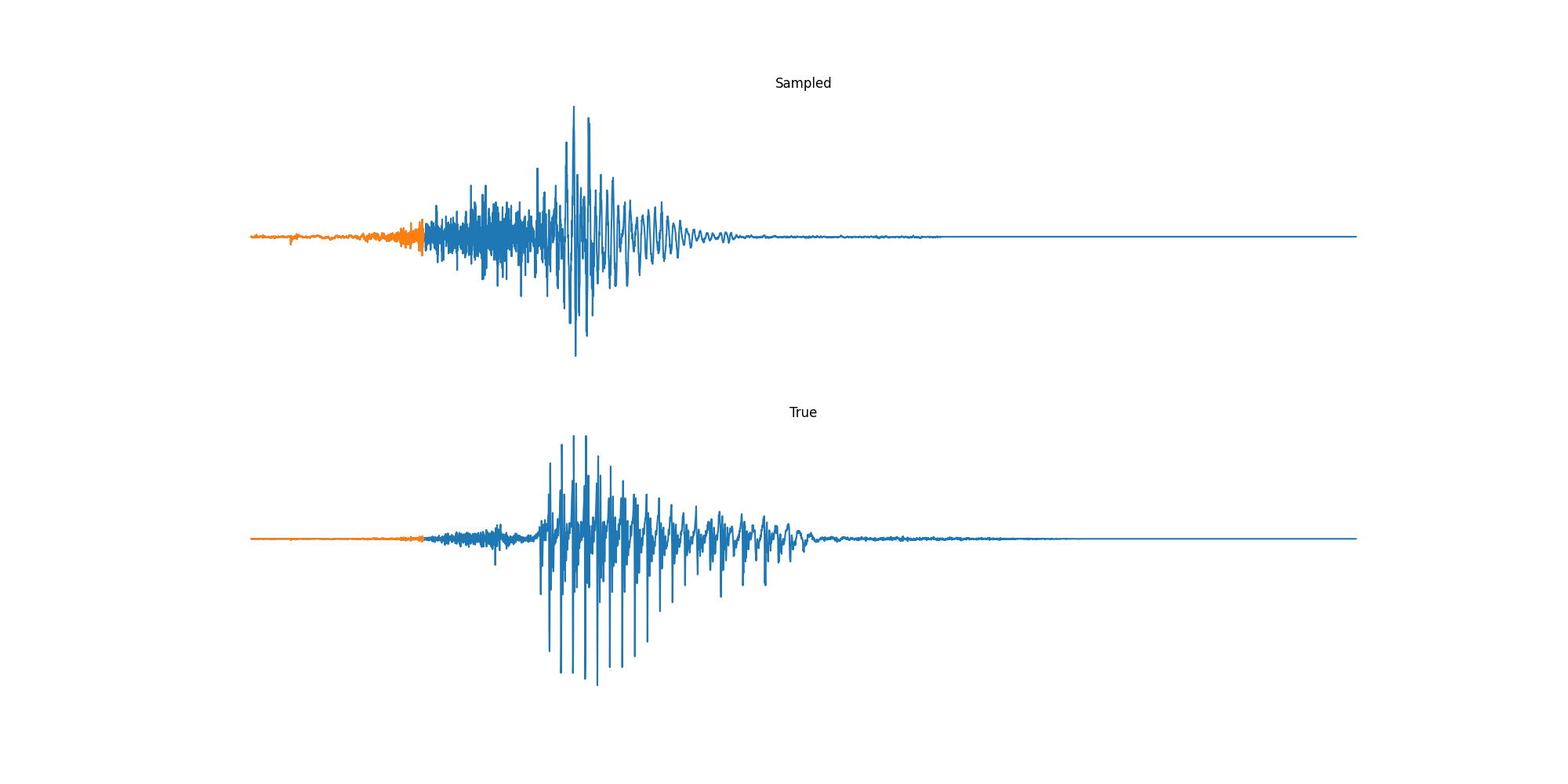
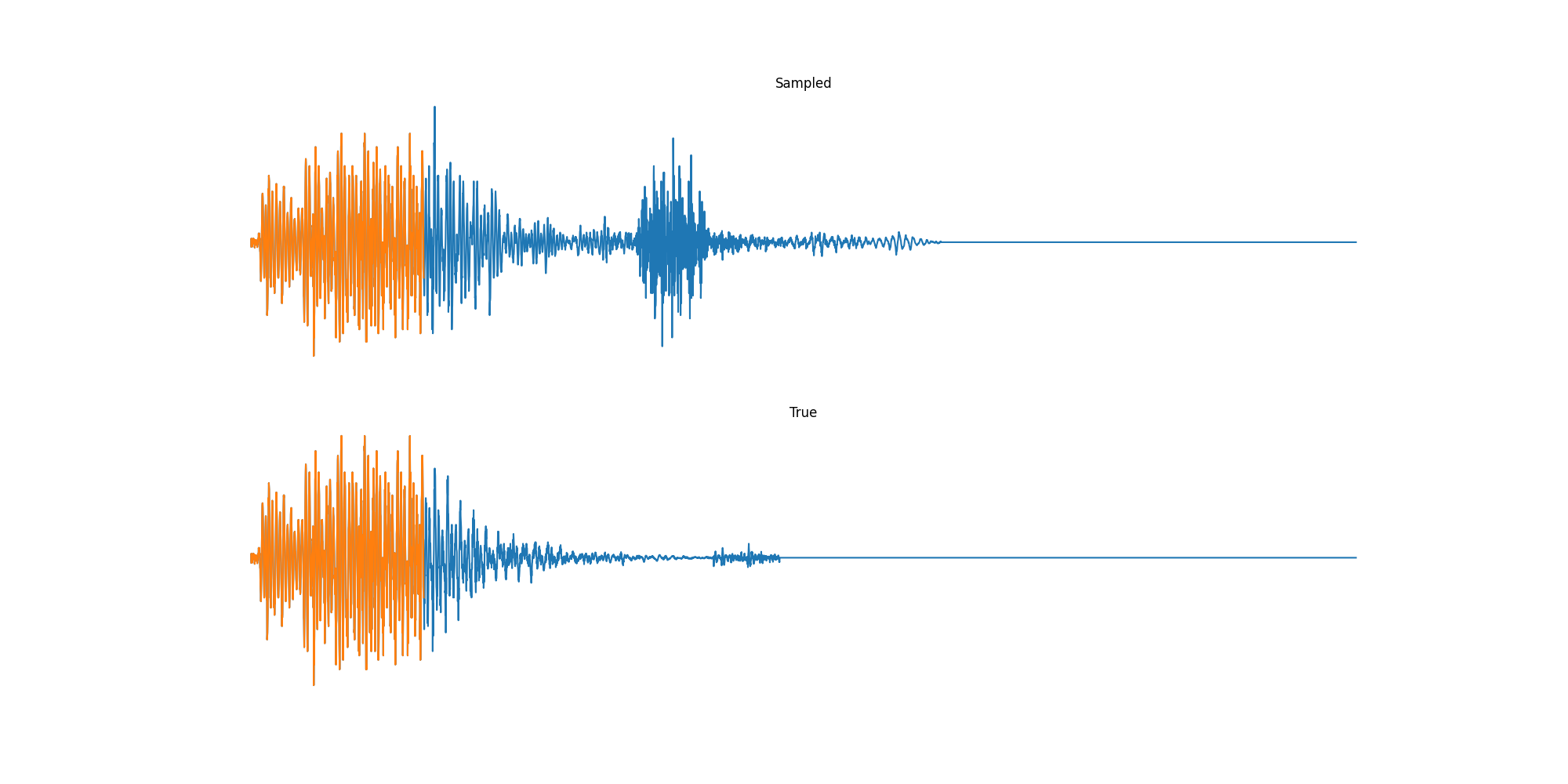
Conclusion & Future Work

Conclusion (on JAX)

  • JAX really signs at modular mathematical code.

  • JAX JIT makes some hard code trivial.

  • Lifting in Flax

New Paper - Diagonal State Spaces.

# Replaces Part 2.
def complex_softmax(x, eps=1e-7):
    def reciprocal(x):
        return x.conj() / (x * x.conj() + eps)

    x2 = x - x[np.argmax(x.real)]
    e = np.exp(x2)
    return e * reciprocal(np.sum(e))

def dss_kernel(W, Lambda, L, step):
    P = (step * Lambda)[:, None] * np.arange(L)
    S = jax.vmap(complex_softmax)(P)
    return ((W / Lambda) @ S).ravel().real

def dss_ssm(W, Lambda, L, step):
    N = Lambda.shape[0]
    Abar = np.diag(np.exp(Lambda * step))
    b = jax.vmap(lambda l:
                 1 / (l * (np.exp(l * np.arange(L) * step)).sum()))
    Bbar = b(Lambda).reshape(N, 1)
    Cbar = W.reshape(1, N)
    return (Abar, Bbar, Cbar)

Thank You

  • Huge thanks to Albert Gu and Karan Goel, who were super helpful in putting this together. Their paper and codebase.

  • Ankit Gupta for helping with his DSS model

  • Thanks to Conner Vercellino, Laurel Orr, Ankit Gupta, Ekin Akyürek, Saurav Maheshkar