By Sasha Rush - Notebook
Built with Chalk developed with Dan Oneață
This is the second part of a series on graphics in Jax. In the first part we built a differentiable renderer.
The focus of this blog post is about the connections between vector graphics and array shapes. This one is a bit less complex, and is more about the programming aspects than the underlying theory.
For this blog, our goal is to render wallpaper in Matplotlib. We will work our way up to this:
Before doing anything interesting, we’ll start by creating some basic shapes. Classically this is an intro exercise in programming classes (think Turtle graphics). In this setting, we draw a shape one segment at a time by putting down a pen and lifting it up.
When programming in vector languages like Jax, we prefer to do things in parallel when possible. Instead of a for loop we can draw each segment of the triangle in parallel and then combine everything together into a shape. (See the previous post for a description of how rotate works.)
@jax.vmap
def draw_tri(i):
return seg(unit_x).rotate(-(i / 3) * 360)Internally, this using the vectorized map to create an array with as many segments as arguments. Here is how we use it.
tri = draw_tri(np.arange(3)).close().stroke()
show(tri.line_width(2))
If we want to apply colors to the shapes we need to first close and stroke them. Then we can apply standard styling.
@jax.vmap
def draw_sq(i):
return seg(unit_x).rotate(-(i / 4) * 360)
square = draw_sq(np.arange(4)).close().stroke()
show(square.line_width(2).fill_color("blue"))
Of course we can make more interesting shapes by parameterizing the function. We use the higher-order function partial to tell vmap which of the axes we should map over and which are fixed args. To make things simpler also include methods for aligning shapes to the axis. This makes it simple to support rotations.
@partial(jax.vmap, in_axes=(0, None))
def draw_poly(i, I):
return seg(unit_x).rotate(-(i / I) * 360)
poly = lambda I: draw_poly(np.arange(10), I).close().stroke().line_width(3)
show(poly(10).center_xy())
Here are a couple of others just for fun.
@jax.vmap
def draw_star(i):
return seg(unit_x).rotate(-(2 * i / 5) * 360)
star = draw_star(np.arange(5)).close().stroke().line_width(2).center_xy()
show(star)
@jax.vmap
def repeat_colors(i):
red, blue = to_color("red"), to_color("blue")
return star.rotate(i *10).line_color((1 -i /10)*red + i/10 * blue)
show(repeat_colors(np.arange(10)).concat())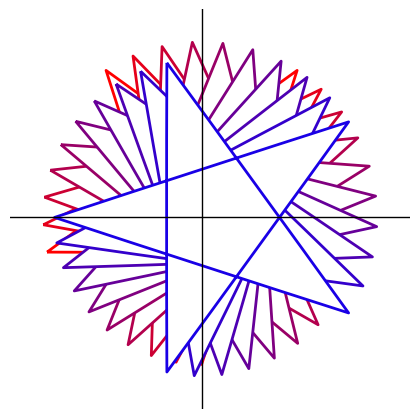
@jax.vmap
def draw_spiro(i):
return seg(unit_x).rotate(-(13 * i / 27) * 360)
spiro = draw_spiro(np.arange(64)).close().stroke().line_width(2).center_xy()
show(spiro)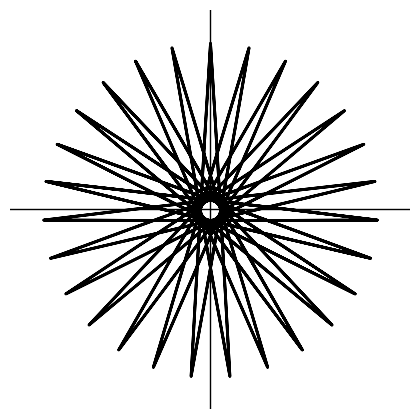
All segments are arc-based curves. If we want to draw actual arcs we use a different segment primitive.
@jax.vmap
def draw_circle(i):
return arc_seg_angle(270, 90).rotate(-(i / 4) * 360)
circle = draw_circle(np.arange(4)).close().stroke().line_width(2).center_xy()
show(circle)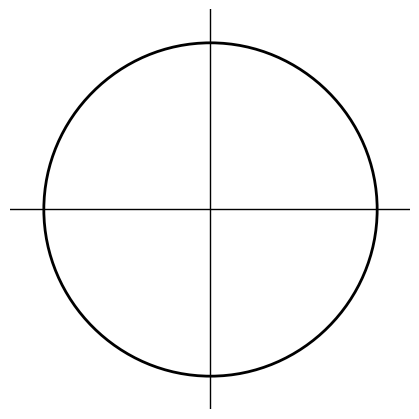
Things get a bit more complex when handling shapes with different part. Here’s an example where we have a shape that is half circle and half line. We can handle this with the switch statement which will act differently based on the value given. Here the half-circle function in the list gets called first and then the line.
@jax.vmap
def draw_halfcircle(i):
return jax.lax.switch(i,
[lambda: arc_seg_angle(180, 180),
lambda: seg(-2*unit_x)]
)
d = draw_halfcircle(np.arange(2)).close().stroke().line_width(2)
show(d)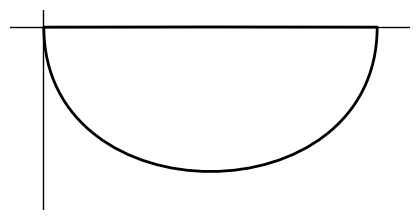
To make a wedge we use three different parts.
@partial(jax.vmap, in_axes=(0, None))
def draw_wedge(i, angle):
return jax.lax.switch(i,
[lambda: seg(unit_x),
lambda: arc_seg_angle(0, angle),
lambda: seg(-unit_x).rotate(-angle)]
)
wedge = draw_wedge(np.arange(3), 45).close().stroke().line_width(2)
show(wedge)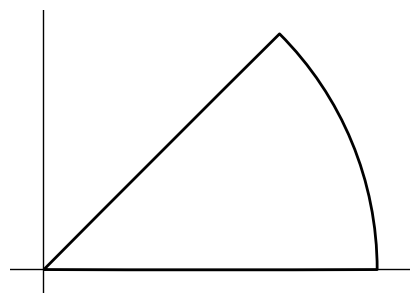
Once we construct shapes using trails we can then compose them together. Critically here the batch is no longer going to represent the connected trails, but instead several different diagrams that we will then concat together.
Here we concat four different hexagons together of different scales.
@partial(jax.vmap, in_axes=(None, 0))
def scale(shape, i):
return shape.center_xy().scale(i)
# Function `arange` is used to create a batch of 4 diagrams
d = scale(poly(5), np.arange(5, 1, -1))
# Concat composes them on top of one another
show(d.concat())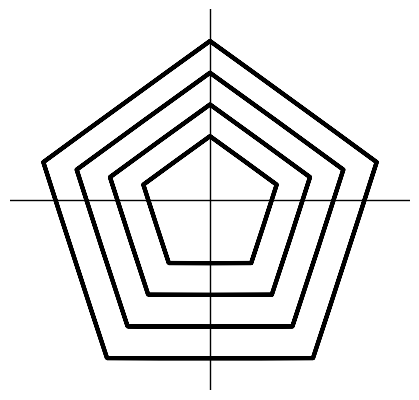
Our goal will be to layout shapes in interesting ways, eventually leading up to full tesselations.
To start with let’s consider an easy example where we just tile our shape in a regular 2D grid with a colormap. We use the Bremm 2D Colormap to get interesting shades.
def colormap(x, y, X=10, Y=10):
"Use the Bremm colormap by position"
return pix[np.round((x + 1)/X * 512).astype(int),
np.round((y + 1)/Y * 512).astype(int)] / 256
def tile(shape_fn, I, J, off_x, off_y, extra=np.array([0])):
@jax.vmap
@jax.vmap
def t(i, j):
return shape_fn(i, j).translate(i * off_x + extra[j % len(extra)],
j * off_y)
# Vmap over two iterators.
return t(*np.broadcast_arrays(np.arange(I)[:, None], np.arange(J)))
show(tile(
lambda i, j: square.fill_color(colormap(i, j)), 10, 10, 1, 1).concat().concat(),
show_ax=False)
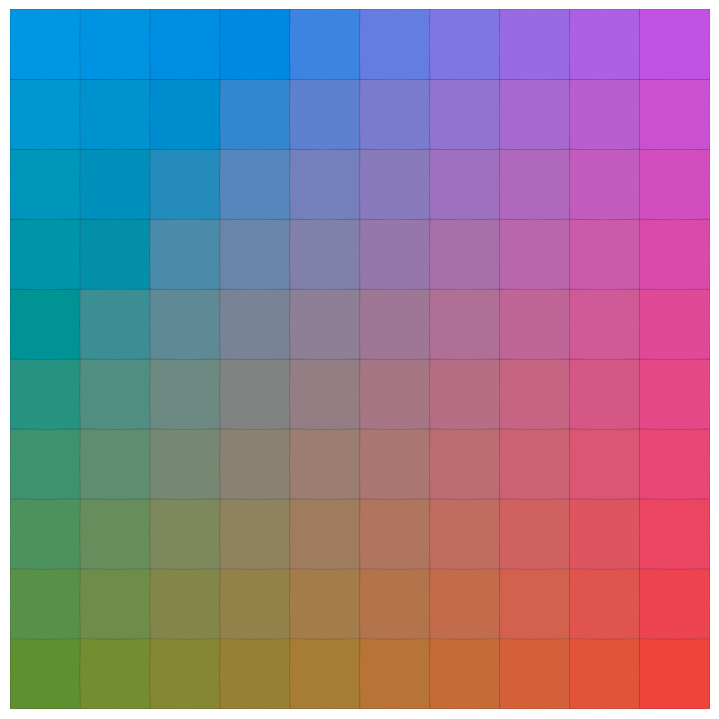
Jax will vectorize over everything so we can be a bit more creative about how we lay things out. Here is an old Pantone photo with circles of different shapes.
show(tile(
lambda i, j: circle.scale(j/20 + i/20 + 0.1).line_width(0).fill_color(colormap(i, j)),
10, 10, 1, 1).concat().concat(),
show_ax=False)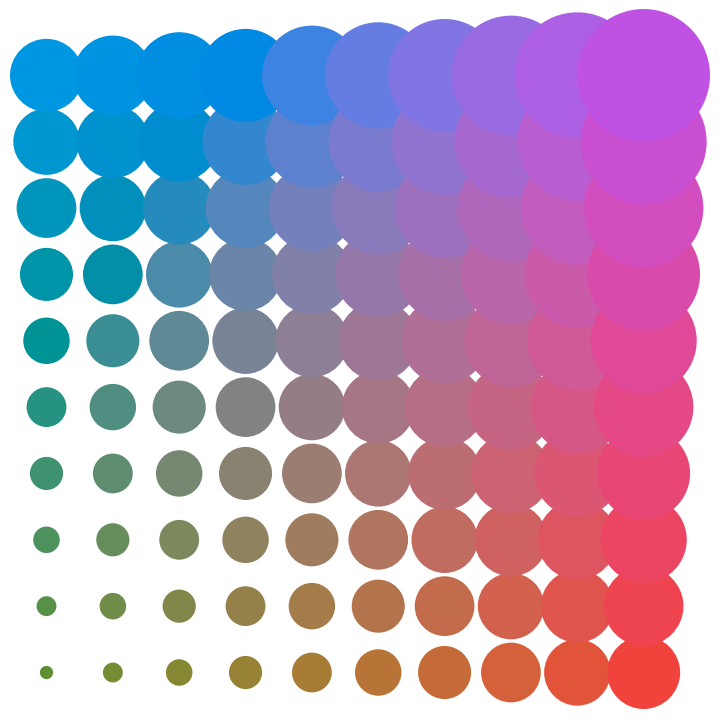
Continuing with the tessalation theme we can use Jax conditionals to have irregular pattern layouts.
I, J = 20, 20
def up_down(i, j):
@jax.vmap
def d(k):
# Rotate every other triangle and change color.
return jax.lax.cond(
k == 0,
lambda: tri.fill_color(colormap(i, j, I, J)),
lambda: tri.rotate(180).align_t().translate(0.5, 0)\
.fill_color(colormap(J-j, i, J, I))
)
return d(np.arange(2)).line_color("white").line_width(2)
til = tile(up_down, I, J, 1, tri.get_envelope().height)
show(til.concat().concat().concat(), show_ax=False)

Since our intermediate diagrams are also Jax objects (specifically PyTrees) we can also use them in other constructs
If we want to layout shapes based on the sizes of their neighbors we need to instead use scan. Here we run a scan that sets the translation of each part of the diagram based on the other elements of the batch.
def step(vec, sep=0):
"Layout along vec separated by sep"
def fn(carry, shape):
"Scan where carry is the translation."
env = shape.get_envelope()
right, left = vec * env(vec), vec * env(-vec)
return carry + right + left + vec * sep, \
shape.translate_by(carry + left + vec*sep)
return fn
def cat(x, v, sep=0):
return jax.lax.scan(step(v, sep), V2(0, 0), x)[1]
# Layout horizontal (unit_x is (1, 0)
hcat = lambda x, sep=0: cat(x, unit_x, sep)
# Layout vertical (unit_y is (0, 1)
vcat = lambda x, sep=0: cat(x, unit_y, sep)
def repeat(diagram, I):
"Makes a batch of diagrams"
@jax.vmap
def rep(i):
return diagram
return rep(np.arange(I))
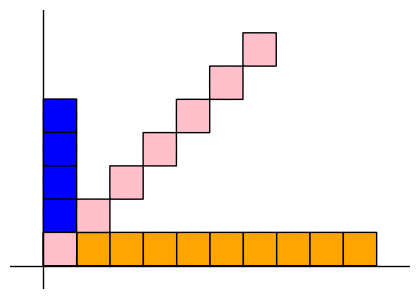
s = square.fill_color("orange").line_width(1)
show(hcat(repeat(s, 10)).concat() +
vcat(repeat(s.fill_color("blue"), 5)).concat() +
cat(repeat(s.fill_color("pink"), 7), unit_y + unit_x).concat())
Similarly to scan, we can also have vmap take in diagrams as input. This allows modifying style properties for the already created image before concatenating to a final figure.
I, J = 15, 5
@jax.vmap
def pattern(i):
order = np.arange(1, I)
# Make a row. Alternate increasing / decreasing
y = hcat(square.center_xy().scale_y(np.where((i % 2) == 0,
order,
np.max(order) + 1 - order)/2 ))
# Align height to the height of the neighbor row.
h0 = y[0].get_envelope().height
h1 = y[-1].get_envelope().height
return y.translate(0, i * (h0 + h1)/ 2)
# Vmap over the batched diagram, setting the color after layout.
@jax.vmap
@jax.vmap
def color(shape, i, j):
return shape.fill_color(colormap(i, j, I, J)).line_width(2)
# Create a batched Diaggram
d = pattern(np.arange(J))
print("Batched diagram shape", d.shape)
# Fill in the colors of the diagram
ind = np.meshgrid(*[np.arange(s) for s in reversed(d.shape)])
show(color(d, *ind).concat().concat(),show_ax=False)Batched diagram shape (5, 14)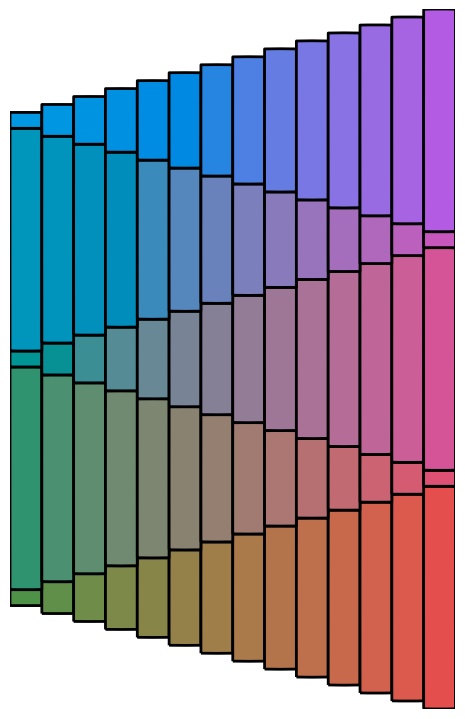
This example uses shape drawing and several of the vectorizing functions we have seen earlier. We use np.where for the conditional coloring.
@jax.vmap
def draw_crescent(i):
return jax.lax.switch(i,
[lambda: arc_seg(V2(1, 0), 1),
lambda: arc_seg(V2(-1,0), -0.5)]
)
crescent = draw_crescent(np.arange(2)).close().stroke().line_width(2).rotate(90)
N = 25
@partial(jax.vmap, in_axes=(None, 0, None))
def rotate(c, i, N):
return c.rotate(i / N * 360)
@jax.vmap
def red_colors(c, i):
red, yellow = to_color("red"), to_color("yellow")
j = i % 5
color = np.where(j == 0, to_color("darkblue"),
(j / 5) * yellow + (1 - (j/ 5)) *red)
return c.fill_color(color)
I = np.arange(N)
shapes = rotate(crescent, I, N)
shapes = red_colors(shapes, I).line_width(0)
show(shapes.concat(), xlim= (-0.5, 0.5), ylim=(-0.5,0.5), show_ax=False)

This one is based on the beautiful mobile game “I Love Hue”. We first create the interlocking ring pattern, then use tiling to lay it out. Gradients are flipped for a group of tiles.
I, J = 10, 30
hex = regular_polygon(6, 1)
def make_shape():
# Inner hexagon
inner = hex.fill_opacity(0.8).line_width(0)
# Ring of triangles
tri = triangle(1).rotate(360 / 12)
tri = inner.juxtapose(tri, -unit_x)
layer_1 = rotate(tri, np.arange(6), 6).concat().fill_opacity(0.4).line_width(0.05)
# Ring of squares
sq = inner.juxtapose(square.center_xy(), -unit_y).fill_opacity(0.1).line_width(0.05)
layer_2 = rotate(sq, np.arange(6), 6).concat()
return inner + layer_1 + layer_2
shape = make_shape()
# Values for row and col height.
d = hex.get_envelope()(unit_y)
d2 = shape.get_envelope()(unit_x)
# Conditional for flipping colors.
def check(i, j):
return ((i > 5) & (i < 9) & (j > 5) & (j < 11) |
(I -i > 5) & (I-i < 9) & (J-j > 5) & (J-j < 11))
exam = tile(lambda i, j: shape.fill_color(colormap(np.where(check(i,j), I-i, i),
np.where(check(i,j), J-j, j),
I, J)),
I, J, 2*d2+1, d+0.5, np.array([0, d2+0.5]))
show(exam.concat().concat(), show_ax=False)
I thought this one was cool. We have an circle gradient with a different inner color. Tiling is pretty simple.
red = to_color("red")
y = to_color("yellow")
I, J = 10, 10
def pc(I):
@jax.vmap
def fill(i):
# Draw the inner circle.
r = I - i + 5
c = circle.scale(r).translate(0, r - r / 5).line_width(0)
return jax.lax.cond(
i == I-1,
lambda: c.fill_color("darkblue"),
lambda: c.fill_color((i / I) * y + (1 - (i/ I)) *red)
)
return fill(np.arange(1, I)).scale(1/I)
p = pc(I).concat()
env = p.get_envelope()
w, h = env.width * 1.2, env.height * 1.2
# Overlay peacock and circle. Offset rows for style.
t = tile(lambda *_:
p.center_xy(), I, J, w, h, np.array([w/2, 0]))
x = tile(lambda *_:
circle.scale(0.35).center_xy().translate(0, 1).fill_color("white").line_width(0),
I, J, w, h, np.array([0, w/2]))
# Add blue background.
result = (square.fill_color("darkblue").scale_x(w * I).scale_y(h * J).center_xy() +
(t + x).concat().concat().center_xy())
show(result, show_ax=False)

I, J = 12, 25
# The symbol | mean "next to".
r = tile(lambda i, j:
square.scale(0.5).fill_color("purple") |
square.fill_color(colormap(i, j)).line_width(2),
I, J, 2.5, 0.5,
-np.arange(J) % 10).concat().concat()
show(r, (10, 20), (1, 12), show_ax=False)
This is a type of recursive tessalation that can be constructed by subdividing a shape repeatedly. We first order the shape and then repeat.
r = square.scale_x(0.5)
@partial(jax.vmap, in_axes=(0, None))
def tessalate(r, s):
# If statement is allowed bacause we do not map over the step.
if s == 0:
c = square.scale_x(0.5).align_t()
else:
c = tessalate(np.arange(4), s-1).concat().align_t()
# Make the dominoes. Juxtapose puts a shape next to another.
return jax.lax.switch(r,
[lambda: c.juxtapose(c.rotate(90), unit_y),
lambda: c.rotate(0),
lambda: c.juxtapose(c, unit_x),
lambda: c.juxtapose(c.rotate(90), -unit_y)]
)
show(tessalate(np.arange(4), 0).concat().rotate(90).line_width(1).fill_color("orange"),
show_ax=False)
show(tessalate(np.arange(4), 4).concat().rotate(90).line_width(1).fill_color("orange"),
show_ax=False)
We’ll end with a famous example of the Penrose Tiling. There are many great explanations of how this works on the web. This version is adapted from this blog.
gr = 2 / (1+np.sqrt(5))
tris = (np.array(0), P2(0, 0) + unit_x,
P2(0, 0) + unit_x + tx.rotation(tx.to_radians(180-36)) @ unit_x,
P2(0, 0))
#@jax.vmap
def penrose(triangle, s):
color, a, b, c = triangle
def blue():
p = a + (b-a) * gr
@jax.vmap
def x(i):
return jax.lax.switch(i,
[lambda: (0, c, p, b),
lambda: (1, p, c, a)])
# Needs to be 3 to match other branch.
return x(np.arange(3))
def red():
q = b + (a-b) * gr
r = b + (c-b) * gr
@jax.vmap
def x(i):
return jax.lax.switch(i,
[lambda: (1, r, c, a),
lambda: (1, q, r, b),
lambda: (0, r, q, a)])
return x(np.arange(3))
next = jax.lax.cond(color==0, blue, red)
if s == 0:
return next
else:
res = jax.vmap(penrose, in_axes=(0, None))(next, s - 1)
# Collapse recursive dimensions to a single dimension.
return (res[0].reshape(-1),
res[1].reshape(-1, 3, 1),
res[2].reshape(-1, 3, 1),
res[3].reshape(-1, 3, 1))
@jax.vmap
def draw(t):
color, a, b, c = t
tri = Path.from_points([a, b, c]).stroke()
return jax.lax.cond(color,
lambda: tri.fill_color("blue"),
lambda: tri.fill_color("red"))
@partial(jax.vmap, in_axes=(None, 0))
def rot(shape, i):
# Mirror every second triangle
return shape.scale_x(np.where(i%2, 1, -1)).rotate(i / 10 * 360)
show(rot(draw(penrose(tris, 7)).concat().rotate(108).center_xy().align_t(),
np.arange(10)).concat(), show_ax=False)

for i in range(1, 7):
d = rot(draw(penrose(tris, i)).concat().rotate(108).center_xy().align_t(),
np.arange(10)).concat()
d.render_mpl(f"penrose{i}.png")





Cheers, - Sasha